Poisson Regression¶
import numpy as np
import matplotlib.pyplot as plt
import vowpalwabbit
%matplotlib inline
# Generate some count data that has poisson distribution
# z ~ poisson(x + y), x \in [0,10), y \in [0,10)
x = np.random.choice(range(0,10), 100)
y = np.random.choice(range(0,10), 100)
z = np.random.poisson(x + y)
We will model this data in two ways
log transform the labels and use linear prediction (square loss)
model it directly using poisson loss
The first model predicts mean(log(label)) the second predicts log(mean(label)). Due to Jensen’s inequality, the first approach produces systematic negative bias
# Train log-transform model
training_samples = []
logz = np.log(0.001 + z)
vw = vowpalwabbit.Workspace("-b 2 --loss_function squared -l 0.1 --holdout_off -f vw.log.model --readable_model vw.readable.log.model", quiet=True)
for i in range(len(logz)):
training_samples.append("{label} | x:{x} y:{y}".format(label=logz[i], x=x[i], y=y[i]))
# Do hundred passes over the data and store the model in vw.log.model
for iteration in range(100):
for i in range(len(training_samples)):
vw.learn(training_samples[i])
vw.finish()
# Generate predictions from the log-transform model
vw = vowpalwabbit.Workspace("-i vw.log.model -t", quiet=True)
log_predictions = [vw.predict(sample) for sample in training_samples]
# Measure bias in the log-domain
log_bias = np.mean(log_predictions - logz)
bias = np.mean(np.exp(log_predictions) - z)
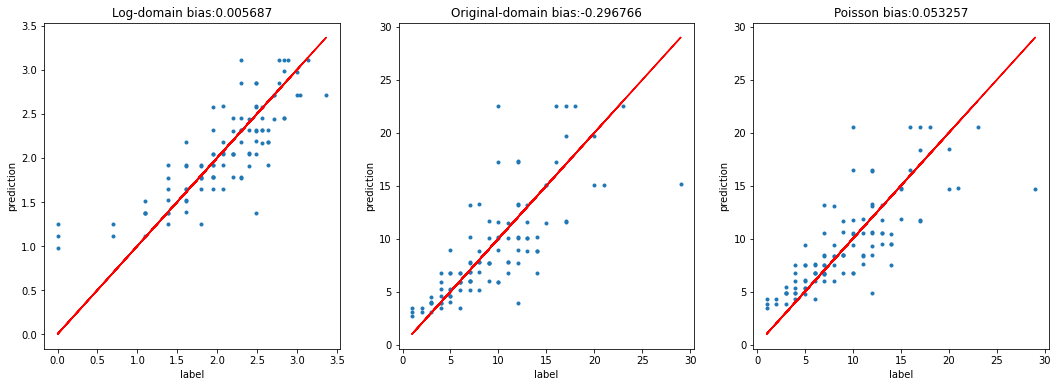
Although the model is relatively unbiased in the log-domain where we trained our model, in the original domain there is underprediction as we expected from Jensenn’s inequality
# Train original domain model using poisson regression
training_samples = []
vw = vowpalwabbit.Workspace("-b 2 --loss_function poisson -l 0.1 --holdout_off -f vw.poisson.model --readable_model vw.readable.poisson.model", quiet=True)
for i in range(len(z)):
training_samples.append("{label} | x:{x} y:{y}".format(label=z[i], x=x[i], y=y[i]))
# Do hundred passes over the data and store the model in vw.log.model
for iteration in range(100):
for i in range(len(training_samples)):
vw.learn(training_samples[i])
vw.finish()
# Generate predictions from the poisson model
vw = vowpalwabbit.Workspace("-i vw.poisson.model", quiet=True)
poisson_predictions = [np.exp(vw.predict(sample)) for sample in training_samples]
poisson_bias = np.mean(poisson_predictions - z)
plt.figure(figsize=(18,6))
# Measure bias in the log-domain
plt.subplot(131)
plt.plot(logz, log_predictions, '.')
plt.plot(logz, logz, 'r')
plt.title('Log-domain bias:%f'%(log_bias))
plt.xlabel('label')
plt.ylabel('prediction')
plt.subplot(132)
plt.plot(z, np.exp(log_predictions), '.')
plt.plot(z, z, 'r')
plt.title('Original-domain bias:%f'%(bias))
plt.xlabel('label')
plt.ylabel('prediction')
plt.subplot(133)
plt.plot(z, poisson_predictions, '.')
plt.plot(z, z, 'r')
plt.title('Poisson bias:%f'%(poisson_bias))
plt.xlabel('label')
plt.ylabel('prediction')
Text(0, 0.5, 'prediction')